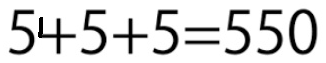- Μηνύματα
- 14.422
- Reaction score
- 12.119
Από το δημοτικό μάθαμε για τη σειρά των πράξεων η οποία ισχύει όπως την ξέρετε (δεν την επαναλαμβάνω) αλλά πολλοί ξεχνάτε τον κανόνα που λέει επίσης για "αριστερά προς τα δεξιά"
Για τους Αγγλομαθείς τα λέει πολύ ωραία εδώ:
 en.wikipedia.org
en.wikipedia.org
Και συγκεκριμένα καταλήγει σε ένα σημείο (τα έντονα δικά μου):
Για τους Αγγλομαθείς τα λέει πολύ ωραία εδώ:
Order of operations - Wikipedia
 en.wikipedia.org
en.wikipedia.org
Και συγκεκριμένα καταλήγει σε ένα σημείο (τα έντονα δικά μου):
Επειδή όμως, λέει, δεν είναι γενικά αποδεκτό αυτό:When evaluating expressions that only include addition and subtraction, such as the expression above, addition and subtraction may be performed sequentially, working left to right, but of the six major arithmetic operations, only addition and multiplication are commutative and associative, and so professionals usually view subtraction, especially in algebra and in higher mathematics, as addition of a negative number. Either working left to right or treating the subtraction as adding a signed number will produce the correct answer; performing subtraction in the wrong order will result in the incorrect answer.
συμπεριφέρεται στη διαίρεση σαν πολλαπλασιασμό με τον αντίστροφο αριθμό και καταλήγει σε κάτι εφαρμόσιμο καθολικά:
Τελικά, σε σοβαρά προβλήματα, μάλλον δε θα δείτε τέτοιες γραφές όπως το post #1, αλλά θα δείτε χρήση παρενθέσεων.The second rule, treating division as multiplication by a reciprocal, greatly reduces the frequency of ambiguous division.
a ÷ b ÷ c × d = a × 1 b × 1 c × d = a b × 1 c × d = a b c × d = a d b c {\displaystyle a\div b\div c\times d=a\times {\frac {1}{b}}\times {\frac {1}{c}}\times d={\frac {a}{b}}\times {\frac {1}{c}}\times d={\frac {a}{bc}}\times d={\frac {ad}{bc}}}
But the only sure way to avoid ambiguity is to use parentheses.